9.a) Szamitastudomany

Veges automatak

Def.: $L$ egy nyelv a $\Sigma$ abece felett, ha elemei veges hosszusagu karaktersorozatok (szavak), ahol a karakterek $\Sigma$-bol valoak.

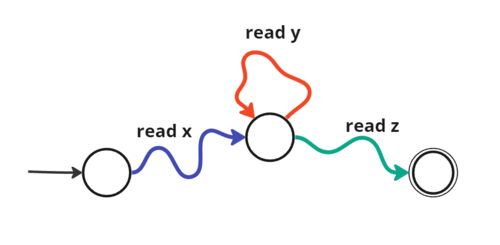
Def.: Az $M=(Q,\Sigma ,\delta ,q_0,F)$ veges automata ahol

• $Q$ – allapotok (veges) halmaza
• $\Sigma$ – az abece ami felett ertelmezve van
• $\delta$ – az atmenet fuggvenye, tehat az adott allapotban valamilyen betut olvas akkor hova kerul
• $q_0$ – a kezdoallapot
• $F$ – az elfogadott vegellapotok halmaza
• $L(M)$ – azon szavak halmaza, amelyek olvasasara $M$ elfogado allapotba kerul

Def.: $M$ felismeri az $L(M)$ nyelvet.
Def.: Egy nyelv regularis ha van veges automata ami felismeri.

Lemma: (Pumpalos-lemma) $\forall L$ regularis $\exists n\forall z\in L$, $|z|\ge n$ $\exists u,v\ne \varnothing$ $w:z=uvw$ es $|uv|\le n$ es $\forall iu{v}^{i}w\in L$

Szavakban, minden regularis $L$ nyelvre letezik elegge hosszu $z$ szo $L$-ben ami felbonthato $3$ reszre: $z=uvw$ ugy hogy a kozepso szot barhanyszor megismetlem, a szo meg mindig $L$-ben lesz, tehat $u{v}^{i}w\in L$ $\forall i\ge 0$.

Megj.: Ha egy nyelv nem pumpalhato akkor nem regularis. Forditva nem igaz, hogy ha egy nyelv pumpalhato akkor regularis.

Turing gep

Def.: Egy $T=(k,\Sigma ,\Gamma ,\alpha ,\beta ,\gamma )$ hatos egy Turing-gep, ahol

• $k\in \mathbb{N}$ – szallagok szama
• $3\le |\Sigma |<\infty$ es $\ast \in \Sigma$ – abece
• $|\Gamma |<\infty$ es $\text{START},\text{STOP}\in \Gamma$ – allapothalmaz
• $\alpha :{\Sigma }^k\times \Gamma \to \Gamma$ – allapot atmenetfuggveny
• $\beta :{\Sigma }^k\times \Gamma \to {\Sigma }^k$ – iras atmenetfuggveny
• $\gamma :{\Sigma }^k\times \Gamma \to (-1,0,1{)}^k$ – fejek mozgasanak az atmenetfuggvenye

Def.: $L$ egy $\Sigma$ feletti nyelv ha $L\subseteq {\Sigma }_0^{\ast }$ ahol ${\Sigma }_0^{\ast }$ a $\Sigma$ abece betuibol kepzett veges sorozatok ($\ast$ nelkul).

Def.: $T$ Turing-gep felismeri az $L\subseteq {\Sigma }_0^{\ast }$ nyelvet ha ${\Sigma }_0^{\ast }$ minden elemen megall es $w\in L$ eseten $1$ az output, $w\in {\Sigma }_0^{\ast }\setminus L$ eseten $0$ az output.

Def.: A $T$ $k+1$ szalagos Turing-gep a szimulalja az $S$ $k$ szalagos Turing-gepet a $p\in {\Sigma }_0^{\ast }$ programmal, ha a $T$ $(k+1)$-edik szalagjara $p$-t irva tetszoleges $w\in {\Sigma }_0^{\ast }$ inputra $T$ es $S$ ugyanakkor all meg vagy nem all meg $w$-n, es megallaskor a $T$ elso $k$ szalagjan ugyanaz van mint $S$-en.

Def.: A $T$ $k+1$ szalagos Turing-gep univerzalis, ha minden $S$ $k$ szalagos Turing-gepehzez letezik $p\in {\Sigma }_0^{\ast }$ program ugy, hogy $T$ szimulalja $S$-et $p$-vel.

Tetel: Minden $k\in \mathbb{N}$ es minden $\Sigma$ abecehez letezik $\Sigma$ feletti $k+1$ szalagos univerzalis Turing-gep.
Biz.: Eloszor belatjuk hogy $k+2$ szalaggal tudunk szimulalni barmilyen $k$ szalagos Turing-gepet.
Irjuk fel $T$ $(k+1)$-edik szalagjara az osszes lehetseges parosat a $k$ hosszu szavaknak $u\in {\Sigma }^k$ es az $S$ lehetseges allapotainak $g\in {\Gamma }_s$. Minden $ug$ parosra odairjuk $S$-nek az atmenet fuggvenyeit is: ${\alpha }_s(u,g),{\beta }_s(u,g),{\gamma }_s(u,g)$.
A $(k+2)$-edik szalagon csak azt taroljuk hogy $S$ eppen milyen allapotban lenne a szimulalaskor.
Igy amikor szimulaljuk $S$-et $T$-n csak annyit kell csinalnunk hogy elkezdjuk olvasni a $(k+1)$-edik szalagot addig ameddig nem talalunk olyan szot ahol $u$ pont az a szo amit olvasunk az elso $k$ szalagrol fentrol lefele. Utana megnezzuk hogy a melle irt allapot megegyezik-e azzal ami a $(k+2)$-edik szalagon van. Ha megtalaltuk azt a bejegyzest a $(k+1)$-edik szalagon amit kerestunk akkor tudjuk hogy $S$ hogyan lepne $u$-t olvasva a $g$ allapotban es ezt tudjuk szimulalni $T$-vel.

Ahoz hogy $k+1$ szalagon is mukodjon a trukk amit csinalunk ugy fogunk tenni mintha ketto fej lenne a $(k+1)$-edik szalagon. Az egyik oldalon $g$-t fogjuk tarolni a masik oldalon az osszes atmenetet. Ahoz hogy tudjunk ket fejet szimulalni egyel ugy trukkozunk hogy minden parosadik cellaba irunk csak betuket mert minden paratlanadikat fentartjuk adminisztraciora. A paratlanadik cellakban $\ast$ vagy $1$-es van azt jeleolve hogy ott van-e a masik fej van nem, $1$ ha ott van, $\ast$ ha nem.

Tetel: Minden $k$ szalagos $S$ Turing-gephez letezik $1$ szalagos $T$ Turing-gep, amely szimulalja $S$-et a kovetkezo ertelemben

• $\forall w\in {\Sigma }_0^{\ast }$ inputra $T$ leall akkor es csak akkor ha $S$ leall $w$-n.
• Leallaskor az $S$ $k$-adik szalagjan ugyanaz van, mint $T$ egyetlen szalagjan (az output megegyezik).
• Ha $S$ leallasig $t$ lepest tett meg, akkor $T$ leallasig $O(t^2)$ lepest tett meg.

Biz.: Gongyuljuk fel a $T$ egyetlen vegtelen hosszu szalagjat $2k$ magasra

RAM gep

Def.: A RAM-gep all egy vegtelen memoriabol, amelynek cellait $X[i]$-vel jeloljuk, minden cellaban egy $\mathbb{Z}$-beli szam irhato. A RAM-gep ezen kivul tratalmaz egy programtarat, amelybe a kovetkezo programsorok barmilyen kombinacioja irhato:

• $X[i]:=0$
• $X[i]:=1$
• $X[i]:=X[i]\pm X[j]$
• $X[i]:=X[i]\pm 1$
• $X[i]:=X[j]$
• $X[i]:=X[X[j]]$
• $X[X[i]]:=X[j]$
• $\text{IF }X[i]\le 0\text{ THEN GOTO [programsor cime]}$

A RAM-gep outputja a veges memoria tartalma. Kezdetben minden celle $0$-ra van inicializalva.

Tetel: Minden $\Sigma =\{0,1,2\}$ folotti egy szalagos Turing-gephez van olyan program a RAM-gepen ami szimulalja a kovetkezo ertelemben:

• $\forall w\in {\Sigma }_0^{\ast }$ inputra a Turing-gep megall akkor es csak akkor ha a RAM-gep megall.
• Megallaskor a ket gepen az output ugyanaz.
• Ha a Turing-gep megallasik $t$ lepest tett meg akkor a RAM-gep $O(t)$ programsort hajt vegre megallasig.

Def.: Egy RAM-gep programjanak logaritmikus koltsege, avagy futasi ideje $u\in \mathbb{N}$ , ahol $u$-t ugy kapjuk hgoy a vegrehajtott programsorok szamat osszegezzuk a bennuk szereplo szamok binaris hosszaval ($x\to \log x$).

Tetel: Minden RAM-gep programhoz an egy olyan $T$ Turing-gep amely azt szimulalja a kovetkezo ertelemben:

• Ugyanazon az inputon allnak meg.
• Ugyanaz az output a ket gepen megallaskor.
• Ha a RAM-gep logaritmikus koltsege $u$ akkor a Turing-gep megallasikg $O(u^2)$ lepest tesz meg.

Eldonthetetlenseg

Def.: Az $L\subseteq {\Sigma }_0^{\ast }$ nyelv rekurziv ha van olyan $T$ Turing-gep amely ${\Sigma }_0^{\ast }$ minden elemen megall es pontosan akkor $1$ az output ha $w\in L$ kulonben $0$.
Def.: Az $f$ fuggveny rekurziv ha letezik olyan $T$ Turing-gep amely ot kiszamolja, azaz $\forall w\in {\Sigma }_0^{\ast }$ inputon leall es leallaskor az output $f(w)$.
Def.: Az $L\subseteq {\Sigma }_0^{\ast }$ nyelv rekurzivan felsorolhato, ha letezik $f$ rekurziv fuggveny melyre $L=\mathrm{Im}(f)$
Def.: Az $L\subseteq {\Sigma }_0^{\ast }$ complement rekurzivan felsorolhato, ha $\bar{L}$ rekurzivan felsorolhato.

All.: Minden veges nyelv rekurziv.
Biz.: Mivel a nyelv veges ezert van leghosszabb elem, ezert felepithetjuk a nyelv szofajat. A szofara mar tudunk Turing-gepet adni.

Tetel: Madjnem minden nyelv nem rekurziv.
Biz.: Megszamlalhatoan sok Turing-gep van, ezert megszamlalhatoan sok rekurziv nyelv. Viszont continuum sok nyelv van.

Tetel: Az $L$ nyelv rekurzivan felsorolhato akkor es csak akkor, ha van olyan Turing-gep amely ${\Sigma }_0^{\ast }$ elemei kozul pontosan $L$-beli szavakon all meg, a tobbin nem all meg.

Tetel: Majdnem minden nyelv nem rekurzivan felsorolhato.
All.: Ha $A$ es $B$ rekurziv, akkor $A\cup B$, $A\cap B$, $A\setminus B$ szinten rekurzivak.
All.: Ha $A$ es $B$ rekurzivan felsorolhato, akkor $A\cup B$ es $A\cap B$ szinten rekurzivan felsorolhatok.
Lemma: $L\in \text{R}⟺L\in \text{RE}$ es $L\in \text{co-RE}$

Tetel: Legyen $T$ egy $2$-szalagos univerzalis Turing-gep a $\Sigma$ abece felett, Legyen $L_T$ azon $w\in {\Sigma }_0^{\ast }$ szavak halmaza, melyekre $T$ leall ha mindket szalagjara $w$-t urink. Ekkor $L_T$ rekurzive felsorolhato, de nem rekurziv.
Biz.: Nyilvan rekurzive felsorolhato ez a nyelv, mert akkor rekurzive felsorolhato egy nyelv ha van Turing-gep amely pontosan a nyelv elemeire all meg, es $T$ pont akkor all meg ha mindket szalagjara $w$-t irunk.
Tehat, az elozo lemma ertelmeben mar csak annyit kell belatnunk hogy $L_T$ komplementere nem rekurzive felsorolhato.
TODO…

Kovetkezmeny: Nincs olyan Turing-gep ami el tudna donteni hogy egy masik Turing-gep leall-e egy szora. Mashogy megfogalmazva, a $(T,w)$ parokat tartalmazo nyelv, ahol $T$ Turing-gep megall $w$-re, nem rekurziv.

Def.: A dominonyelv szavai dominokeszletek ahol egy dominokeszlet elemei $(a,b,c,d)$ negyesek.
Def.: $L_{\text{KIRAK}}$ azon szavakat tartalmazza a dominonyelvbol amelyekkel lehet parkettazni a sikot.
Def.: $L_{\text{NEMKIRAK}}$ azon szavakat tartalmazza a dominonyelvbol amelyekkel nem lehet parkettazni a sikot.

Lemma: $V$ rekurziv es $L\subset V$. Ekkor $L$ rekurziv akkor es csak akkor ha $L$ es $V-L$ rekurzive felsorolhato.
Tetel: $L_{\text{NEMRAK}}$ rekurzive felsorolhato.
Lemma: $w\in L_{\text{KIRAK}}⟺w$-vel kirakhato minden $N\in \mathbb{N}$ szmara a $(2N+1)\times (2N+1)$ meretu negyzet.
Tetel: $L_{\text{KIRAK}}$ nem rekurzive felsorolhato.

Bonyolultsagi osztalyok

Def.: ${\mathrm{time}}_T(n)$ jeloli a legfeljebb $n$ hosszu inputokon hasznalt lepesszamok maximumat a $T$ Turing-gep altal.
Def.: ${\mathrm{space}}_T(n)$ jeloli a legfeljebb $n$ hosszu inputokon hasznalt mezok maximumat a $T$ Turing-gep altal.
Def.: $\mathrm{DTIME}(f(n))$ jeloli azon $L$ nyelvek osztalyat, ahol minden $L$-hez letezik $T$ Turing-gep amely felismeri $L$-et es $w\stackrel{?}{\in }L$ kerdest $f(|w|)$ lepesben eldonti.
Def.: $\mathrm{DSPACE}(f(n))$ jeloli azon $L$ nyelvek osztalyat, ahol minden $L$-hez letezik $T$ Turing-gep amely felismeri $L$-et es $w\stackrel{?}{\in }L$ kerdest $f(|w|)$ tarban eldonti.
Def.:

$$P=\bigcup _{i=1}^{\infty }\mathrm{DTIME}(n^i)$$

Def.:

$$\mathrm{PSPACE}=\bigcup _{i=1}^{\infty }\mathrm{DSPACE}(n^i)$$

All.: $k\cdot {\mathrm{time}}_T(n)\ge {\mathrm{space}}_T(n)$. Kovetkezmenykent $\mathrm{DTIME}(f(n))\subset {\cup }_{k=1}^{\infty }\mathrm{DSPACE}(k\cdot f(n))$.

Def.: $\mathrm{NTIME}(f(n))$ jeloli azon $L$ nyelvek osztalyat, ahol minden $L$-hez letezik $T$ nem determinisztikus Turing-gep amely felismeri $L$-et es $w\stackrel{?}{\in }L$ kerdest $f(|w|)$ lepesben eldonti.
Def.: $\mathrm{NSPACE}(f(n))$ jeloli azon $L$ nyelvek osztalyat, ahol minden $L$-hez letezik $T$ nem determinisztikus Turing-gep amely felismeri $L$-et es $w\stackrel{?}{\in }L$ kerdest $f(|w|)$ tarban eldonti.
Def.:

$$\mathrm{NP}=\bigcup _{i=1}^{\infty }\mathrm{NTIME}(n^i)$$

Def.:

$$\mathrm{NPSPACE}=\bigcup _{i=1}^{\infty }\mathrm{NSPACE}(n^i)$$

Def.: $co-NP=\{l:{\Sigma }_0^{\ast }-L\in \mathrm{NP}\}$

Def.: Azt mondjuk hogy $w$-nek az $L$-beli tagsagara az $y$ szo polinomialis tanu, ha $L$-hez van olyan $T$ Turing-gep, hogy $w\in L⟺T$ elfogadja a $(w,y)$ part $|w|$-ben polinomialis idoben.

Tetel: $L\in \mathrm{NP}$ akkor es csak akkor ha $\forall w\in L$-ra letezik polinomialis tanu.

Tetel: (Pratt) $\mathrm{PRIM}\in \mathrm{NP}$

NP-teljesseg

Def.: Az $L$ nyelv NP-teljes, ha $L\in \text{NP}$ es $\forall K\in \text{NP}$-re ihaz hogy polinomialisan visszavezetheto $L$-re. Azaz $\forall K\in \text{NP}:K\propto L$.

Megj.: Az hogy $L$ NP-teljes nem azt jelenti hogy nehezebb barmilyen masik NP-beli nyelvnel, hanem csak annyit jelent hogy legalabb annyira nehez. Ha azt akarjuk belatni hogy $L$ NP-teljes ahoz kell talalnunk egy $V$ NP-teljes nyelvet es megmutatnunk hogy $V$ visszavezetheto $L$-re. Igy mivel $V$ NP-teljes ezert minden NP nyelv visszavezetheto ra es $V$ visszavezetheto $L$-re. Roviden $\forall K\in \mathrm{NP}:K\propto V\propto L⟹K\propto L$.

Tetel: (Cook) A SAT nyelv NP-teljes.
Biz.: Eloszor is $\mathrm{SAT}\in \text{NP}$, mert egy kielegito behelyettesites polinomialis tanu.
Masodszor annyit kell megmutatnunk hogy barmilyen $T$ nem determinisztikus Turing-gephez tudunk konstrualni olyan konjunktiv normal format, ami pont ennek a gepnek a mukodeset tukrozi. Ez a nehezebb resz a bizonyitasban, de az osszes lepes elegge egyertelmu csak vegig kell gondolni az osszes szabalyat a Turing-gepeknek es azt formalizalni konjunktiv normal formaban.

Visszavezetesek

Tetel: H2C NP-teljes
Tetel: G3C NP-teljes
Tetel: G$k$C NP-teljes
Tetel: INDEPENDENT NP-teljes
Tetel: SAT-3 NP-teljes
Tetel: LEFOG NP-teljes
Tetel: LEFED NP-teljes
Tetel: K-PART NP-teljes
Tetel: PART NP-teljes
Tetel: SUBSET-SUM NP-teljes
Tetel: Hatizsak feladat NP-teljes