1. Huffman kódolás

Egy Texasi kiskocsmaban, Billie-nek a konyvelonek van egy gepe amin vannak billentyuk (0, …, 9, space) amin le kell konyvelnie, hogy melyik ugyfel mennyit fizetett.

Kitor egy lovoldozes a kiskocsmaban es kilovik Billienek az egyik billentyujet. Na de most hogyan konyveljen Billie.
Megoldas: Egy kisebb szamrendszerben konyvel es a kimarado billentyu jatsza majd a szerepet a kilott billentyunek.

Folytatodik a sztori es sorba lovik ki a tobbi billentyut is. Egeszen addig ameddig csak a 0, 1, 2 billentyuk maradnak.

Kilovik a 2-es billentyut is. Mostmar csak 0 es 1-es billentyuk vannak.

• Leir annyi 1-est amennyit fizettek es a 0-as lesz a valaszto karakter.
• mapping: {0: 00, 1: 11, 2: 01} es igy csinalja ugyanazt amit csinalt 3 szamjeggyel

Kilovik az 1-es billentyut is :’(

• kodolja el az egyik elozo kodolasban es irjon le annyi 0-ast amekkora az a szam volt

Tegyuk fel, hogy a fizetesek: ${\alpha }_1,{\alpha }_2,\dots$ ezekbol letrehozza a $\prod p_i^{{\alpha }_i}$ szamot es ezt kodolja

Kovetkezo feladat

$x\in \{0,1{\}}^n$
$\sum x_i=k$
tehat van egy $n$ bites szamunk ahol $k$ darab $1$-es van es ezt szeretnenk lekodolni

Elso eset: $n,k$ fixek/rogzitettek, ekkor eleg $\log \left(\genfrac{}{}{0ex}{}{n}{k}\right)$ bit mivel $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ helyen lehet a $k$ darab $1$-es es ezeket kell csak kodolni

Masodik eset: nem ismerjuk egyiket sem
Ekkor le kell eloszor kodolni az $n$-et utana le kell kodolnunk a $k$-t utana $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ -t
igy ugy fog kinezni, hogy $n$ kodolva ‘vesszo’ $k$ kodolva ‘vesszo’ utolso tag kodolva
a vesszoket el lehet hagyni ha a fenti mappinget hasznaljuk (az utolso tagot nem kell duplazni, mert ott mar nincsen vesszo)
igy fog kijonni a $2\log n$, $2\log k$, $\log \left(\genfrac{}{}{0ex}{}{n}{k}\right)$

ugyesebb megoldas:
(elso $2\log \log n$ bit kodolja az $n$ kodolosanak a hosszat), ($01$), ($2\log \log k$ bit kodolja a $k$ kodolajanak a hosszat), ($01$), ($n+k+\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ kodolva)

osszesen:
$\log \left(\genfrac{}{}{0ex}{}{n}{k}\right)+\log n+\log k+4\log \log n+4$

legyen $p=\frac{k}{n}$ ($0<p<1$)
ebben az esetben a fenti (‘osszesen’) $<(-p\log p-(1-p)\log (1-p))\cdot n+O(\log n)$

Legyen $\underline{p}=(p_1,p_2,\dots ,p_m)0<p_i\le 1\sum p_i=1$

Def.: A kovetkezo mennyiseget a $p$ eloszlas entropiajanak nevezzuk: $H(\underline{p}):=\sum -p_i\log p_i$

Megj.: Valamilyen ertelemben ha egy bitosorozatnak kicsi az entropiaja akkor azt jol lehet kodolni.

All.: Ha $n$ rogzitett, akkor a $H(\underline{p})$ a legnagyobb az $\left(\frac{1}{m},\dots ,\frac{1}{m}\right)$ eloszlason es itt $H(\underline{p})=\log m$

Tegyuk fol, hogy van egy $n$ alapu ABC, tehat $|\Sigma |=n,\forall h\in \Sigma \to p_h$ relativ gyakorisag

Tetel: $x\in {\Sigma }^n$ elkodolhato $\le \frac{H(\underline{p})}{\log m}\cdot n+O\left(\frac{m\log n}{\log m}\right)$ bittel.

Informacioelmeleti also korlat
$N$ kulonbozo dolog elkodolasakor (injektiven) letezik egy olyan kod, ami $\ge \log N-1$ bit
Mivel ${\sum }_{i=0}^n{2}^i=2^{n+1}-1$

Grafok kodolasa

1. Tegyuk fel, hogy $n$ ismert, tovabba, hogy egyszeru es iranyitatlan a graf. Ekkor $\left(\genfrac{}{}{0ex}{}{n}{2}\right)$ bittel el lehet kodolni (az adjecencia matrix felso haromszoge).
2. Tegyuk fel, hogy $m\ll n$ ebbol nagyjabol az kovetkezik, hogy $m\cdot \log \left(\genfrac{}{}{0ex}{}{n}{2}\right)$
   • Ha $n$ ismert, akkor a fentit ki tudjuk szamolni es igy el tudjuk kodolni $m$ darab $\log \left(\genfrac{}{}{0ex}{}{n}{2}\right)$ kodolossal ami megmondja, hogy az $i$.-edik el melyik ket csucsot koti ossze.
   • Ha $n$ nem ismert, akkor $k:=\log \left(\genfrac{}{}{0ex}{}{n}{2}\right)$ es $2\log k+2$ bittel kodoljuk a $k$-t es utana az elozo szerint kodolunk. Igy $m\cdot k+2\log k+2$ bit eleg.

Huffman

A Huffman kod egy betukod, tehat az ABC minden betujehez hozzarendel egy kodot, invjektiven.
$c:\Sigma \to \{0,1{\}}^{\ast }$ inkektiv

Azt szeretnenk hogy a gyakori betuknek legyen rovidebb a kodja, mint azoknak a betuknek amiket alig hasznalunk.

Def.: $c$ kod prefix mentes, ha barhogy veszek ket kukonbozo betut $\forall a\ne b\in \Sigma$ akkor $c(a)$ nem prefixe $c(b)$-nek. Tehat $c(b)$ nem ugy kezdodik, hogy $c(a)$.

Szotar: gyokeres binaris fa es helyenkent vannak levelei. A levelekhez hozzarendelem az ABC elemeit.

Huffman kod:
$\Sigma =\{a_1,a_2,\dots ,a_m\}$, $a_i$ betu gyakorisaga $p_i$ tehat $r_i=p_i\cdot n$ darab van $a_i$-bol a szovegben

Kodolo algoritmus:

1. Letrehozunk $m$ darab levelet, amik reprezentaljak az $m$ darab betut. Minden levelre rairjuk az elofordulasaik szamat, $r_i$-t.
2. Osszevonunk ketto gyokeret, melyeknek a szama a legkisebb. Igy az uj letrehozott gyokernek a szama a ketto masik osszege lesz.
3. Iteraljuk a masodik lepest ameddig tudjuk, tehat mar csak egy gyoker van es osszefuggo a fa.

Miutan letrehoztuk a huffman fat, elnevezzuk a balra nezo agakat $0$-nak es a jobbra nezo agakat $1$-nek. Igy egy betu kodja a gyokerbol a hozzatartozo levelbe mutato ut lesz, nullasokkal es egyesekkel reprezentalva.

Tetel: A Huffman kod hossza minimalis a prefixmentes betukodok kozott

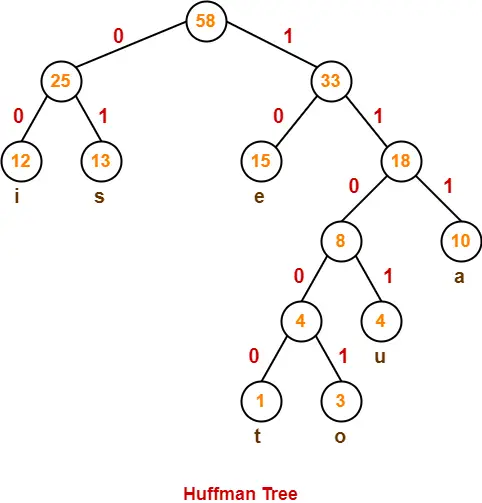
pelda:
A kovetkezo Huffman faban az u betunek a kodja a kovetkezo $1101$