7. FPT algoritmusok

Minimalis koltsegu lefogo csucshalmaz
Minden csucsnak van egy nem negativ koltsege: $w:V\to \mathbb{N}$

legyen valtozok: $x_v\forall v\in V$

$$\begin{array}{rlr}{x}_u+x_v& \ge 1& \forall uv\in E\\ x_v& \ge 0& \forall v\in V\\ x_v& \in \mathbb{N}& \forall v\in V\\ \min & \sum w(v)\cdot x_v& \end{array}$$

Ennek az IP feladatnak az LP relaxaltja (tort relaxaltja) csak annyi, hogy elhagyjuk az egeszsegi feltetelt.

IP feladat optimalis megoldasas: $\text{OPT}$
LP feladat optimalis megoldasa: ${\text{OPT}}^{\ast }$

Eszrevetel 1: ${\text{OPT}}^{\ast }\le \text{OPT}$
legyen $x_v$ a kovetkezo:

$$x_v=\{\begin{array}{ll}1,& \text{ha }{x}_v^{\ast }\ge \frac{1}{2}\\ 0,& \text{kulonben}\end{array}$$

Eszrevetel 2: $\forall uv\in E:x_u+x_v\ge 1$
Eszrevetel 3: $\forall v:x_v\le 2\cdot x_v^{\ast }$

$${\text{OPT}}^{\ast }\le \text{OPT}\le \sum w(v)\cdot x_v\le \sum 2\cdot w(v)\cdot x_v^{\ast }=2\cdot {\text{OPT}}^{\ast }$$

Tehat ez egy $2$-kozelito algoritmus.

Fixed parameter Tractable (FPT)

Input: $(x,k)$ ahol $x$ egy $n$ bites szam (vagy egy $n$ csucsu graf), es $k\in \mathbb{N}$ egy parameter.

peldaul: Kapunk egy $G$ grafot es egy $k\in \mathbb{N}$ paramteret es a kerdes az hogy van e legalabb $k$ hossz ut a $G$ grafban.

Def.: XP azon feladatok halmaza, melyeket meg tudunk oldani polinomialis idoben minden fix $k$-ra.

Def.: FPT $\subseteq$ XP ahol FPT azon feladatok halmaza, melyekre $\exists O(f(k)\cdot n^c)$ ideju algoritmus ami megoldja.

peldaul az elozo orarol a Vertex Cover algoritmus:

VC(G', k'):
	IF k' < 0 THEN return False
	let v in V such that d(v) is maximal
	IF d(v) = 0 THEN return {}  // case: empty graph
	IF k' = 0 THEN return False
	IF d(v) = 1 THEN return tau(G')
	
	// v lefogo
	T_1 := VC(G' - v, k' - 1)
	IF T_1 != False THEN return (T_1 U {v})

	// v nem lefogo
	T_2 := VC(G' - v - N(v), k' - d(v))
	IF T_2 != False THEN return (T_2 U N(v))

Legyen $T(k)$ a rekurziv hivasok szama $k$-ra
Ekkor lathato, hogy $T(k)\le T(k-1)+T(k-2)$

Tehat $O({\varphi }^k\cdot m)$ a futasi ido, mert egy lepest minding meg tudunk csinalni $m$ idoben es a rekurziv hivasok szama a fenti eszrevetel miatt a fibonacci sorozat altal korlatozott.

Tudjuk egy kicsit javitani az algoritmus ugy, hogy atcsereljuk a kovetkezo sort: IF d(v) = 1 ... arra, hogy IF d(v) = 2 ... es igy a rekurziv lepesek szamara igaz, hogy $T(k)\le T(k-1)+T(k-3)$
Igy a futasi ido $O(1.466^k\cdot m)$. Ezt lattuk az elozo oran.

Def.: Egy $(G,k)$ inputu feladat $g(k)$-kernele:
polinomialis idoben elkeszitunk egy $(G^{\prime },k^{\prime })$ inputot, amire:

• Az eredeti feladatra “Igen” a valasz $⟺$ A vesszos feladatra “Igen” a valasz
• $|G^{\prime }|\le g(k)$
• $k^{\prime }\le k$

A lenyege a kernel keszitesnek az, hogy ha tudunk adni egy $g(k)$ kernelt egy feladatra, akkor azt a kernelt barhogyan megoldjuk az algoritmus ami eloszor elkesziti a kernelt es utana a kernelt megoldja biztosan FPT algoritmus lesz. Mivel polinomialis idoben adunk egy $g(k)$ kernelt, es a $g(k)$ meretu feladatot barhogyan megoldjuk, ezert az algoritmus futasideje $O(f(g(k))\cdot poly(n))$, ahol $f$ jeloli a kernel megoldasanak idejet es $poly(n)$ a kernel letrehozasanak idejet.

Kernel keszites a lefogo csucshalmaz feladatra
Feladat: Keszitsunk egy $k$ csucsu lefogo csucshalmazt.
Ha $\exists v:d(v)>k⟹(G^{\prime },k^{\prime }):=(G-v,k-1)$

Megj.: Ha $k<0$ akkor megallunk es az a valaszunk, hogy “Nem lefoghato”.
Megj.: Az izolalt csucsokat toruljuk.

Legyen $k^{\prime }$ a vegso $k$ es $G^{\prime }$ a vegso graf.
Ha $G^{\prime }$-nek tobb mint $k^{\prime 2}$ ele van, akkor megallunk es az a valaszunk, hogy “Nem lefoghato”.
Ha $G^{\prime }$-nek tobb mint $k^{\prime 2}+k^{\prime }$ csucsa van, akkor megallunk es az a valaszunk, hogy “Nem lefoghato”.

Ha ezek utan meg mindig nem alltunk meg, akkor $(G^{\prime },k^{\prime })$ lesz a kernelunk ahol $|V^{\prime }|\le k^{\prime 2}+k^{\prime }$ es $|E^{\prime }|\le k^{\prime 2}$
Ezt a kissebb grafot a fenti algorimussal meg lehet mar oldani $O(1.466^k\cdot k^2)$ lepesben es a kernelt el tudjuk kesziteni $O(m+n)$ idoben.

Def.: $G$ korona-felbontasa: $V=C\cup H\cup B$ (crown, head, body)

1. $C$ fuggetlen
2. $\nexists bc\in E$ ha $b\in B$ es $c\in C$ (a korona es a body kozott nincs el)
3. A $(C,H)$ paros grafban letezik $H$-t fedo parositas
   

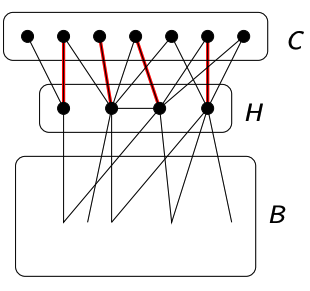
Korona redukcio:

$$(G,k)\to (G[B],k-|H|)$$

ahol $G[B]$ a $G$ graf megszoritasa a $B$ halmazra.

All.: $\tau (G)\le k⟺\tau (G[B])\le k-|H|$
Biz.:
$⟸$ Ha van egy $T\subseteq B$ csucshalmazom, ami lefogja $G[B]$ eleit es $|T|\le k-|H|$, akkor $T\cup H$ lefogja $G$ eleit.

$⟹$ Legyen $T\subseteq V$ egy $G$ eleit lefogo csucshalmaz, amire $|T|=k$.
Ekkor letezik $T^{\prime }$ ugy, hogy $|T^{\prime }|=k$ es $T^{\prime }\cap C=\varnothing$ es $H\subseteq T^{\prime }$, mert a korona felbontas 3. pontja szerint letezik $H$-t fedo parositas a $(C,H)$ paros grafban.

$2k$ csucsu kernel
$G\mapsto P=(V_1\cup V_2,E^{\prime })$

$P$-ben $M$ legnagyobb parositas, $T$ legkisebb lefogo.

Ha $|M|\ge 2k+1$ akkor megallunk. Ezt eldontottuk $O(k\cdot m)$ idoben.

Kulonben elkeszitjuk a kovetkezo koronafelbontast:

$$H:=\{v\in V:v_1\in T,v_2\in T\}$$ $$B:=\{v\in V:v_1\in T-H_1,v_2\in T-H_2\}$$ $$C:=V-H-B=\{v\in V:v_1\notin T,v_2\notin T\}$$

Allitasok:

1. $C$ fuggetlen
2. nem letezik $cv$ el, ahol $c\in C$ es b inn B
3. Az $M$ a $H_1$-et felparositja $C_2$-be
   Igy $G$-ben is *pipa*

$$|B|+2|H|=|T|\le 2k\to |B|\le 2k$$

Igy $(G[B],k-|H|)$ a kernelunk.